
○들어가는 글
우리는 지금까지 tree(이진 트리) 알고리즘과 greedy 알고리즘을 알아보았습니다. 이제 우리는 이 2가지 알고리즘 (이진트리 + 근사 알고리즘) 을 이용해서 좀 더 효율적인 knapsack 알고리즘을 만들어 보려고 합니다. 오늘의 경우는 구현 부분보다는 이론적으로 어떻게 만들 것인지의 대해서 설명해 보겠습니다.
○ 재귀로 구현한 knapsack 알고리즘
우리는 재귀로 구현한 tree 알고리즘으로 knapsack 알고리즘을 구현해 본 적 있습니다. 우선 간단하게 knapsack 알고리즘에 대해 짚고 넘어가도록 하죠 아랫글을 읽으셨다면, 그냥 넘어가셔도 상관없습니다.
이전 내용 : https://kuck-su-labor.tistory.com/52?category=968397
각각 W의 무게와 가치 V를 가지는 물건들이 N개 존재한다고 할 때, 한정된 K의 무게를 담을 수 있는 가방에 최대의 가치의 합이 되도록 담는 방법을 구하라
정해진 공간에 가능한 많은 가치를 가질 수 있도록 담는 문제입니다.

이러면 우리는 재귀로 표현한 완전 탐색 트리 알고리즘으로 구현해 봤습니다. 모든 경우의 수를 구하고, 그중에서 가장 큰 가치의 경우를 찾으면 그만입니다. 한번 실제로 어떤 값이 나오게 될까요? 우선 우리가 실제로 트리를 만들어 본다면 다음과 같은 결과가 나오게 될 것입니다.

그리고 이를 코드로 간단히 구현해 봅시다. 우리가 지금까지 한 것처럼, 재귀로 구현해 봅시다.
var MaxV : Int = 0
fun main() {
val K : Int = 7 // 가방의 크기
val WnV = mutableListOf(3 to 5, 4 to 5, 2 to 3 , 3 to 4) // 각각의 아이템 -> Pair<무게,가치>
println("아이템 : $WnV \n")
print("순회 : ")
Knapsack(WnV,7,0,0)
println("\n")
println("최댓값 : $MaxV")
}
// 재귀로 구현하는 완전탐색
fun Knapsack(VA : MutableList<Pair<Int, Int>> , K : Int , i : Int , VM : Int) : Int { // 배열, 총 무게, 인덱스, 축척된 가치
if(K < 0) return 0 // 무게를 초과하지 못하도록 하기 위해서
print("-> $VM ")
if(K <= 0 || i >= VA.size) {
if(VM> MaxV) MaxV = VM // 기존의 최댓값과 비교하면서 더 큰 최댓값이 있다면 변경한다.
return 0
}
Knapsack(VA,K-VA[i].first,i+1,VM+VA[i].second) // 노드의 좌측방향 (물건을 담는경우)
Knapsack(VA,K,i+1,VM) // 노드의 우측방향 (물건을 담지 않는 경우)
return 0
}

순회 방법은 print문을 맨 위에 썼기 때문에 전위순회 순으로 읽으시면 됩니다. 그리고 이를 대입해보면, 올바르게 나오고 있다는 것을 알 수 있습니다.
○ 재귀로 구현한 knapsack 알고리즘의 개선
이렇게 구현하게 되면 가장 큰 문제는 비용입니다. 완전 탐색은 앞에서 설명해 드렸듯이 비용이 효율적이지 않습니다. 따라서 이러한 단점을 보완하기 위해서 우리는 greedy 알고리즘을 사용할 수 있습니다. (정확히는 greedy 알고리즘을 근사 알고리즘으로 활용합니다. )

예를 들어봅시다. 다음에서 순회를 해서 우리는 어느 정도 해가 되는 값을 찾은 것 같습니다. 아래의 그림에서 붉은색으로 표시된 부분은 지금까지 순회한 부분에서 가장 해답에 근접합니다. (그리고 실제로도 정답입니다.)
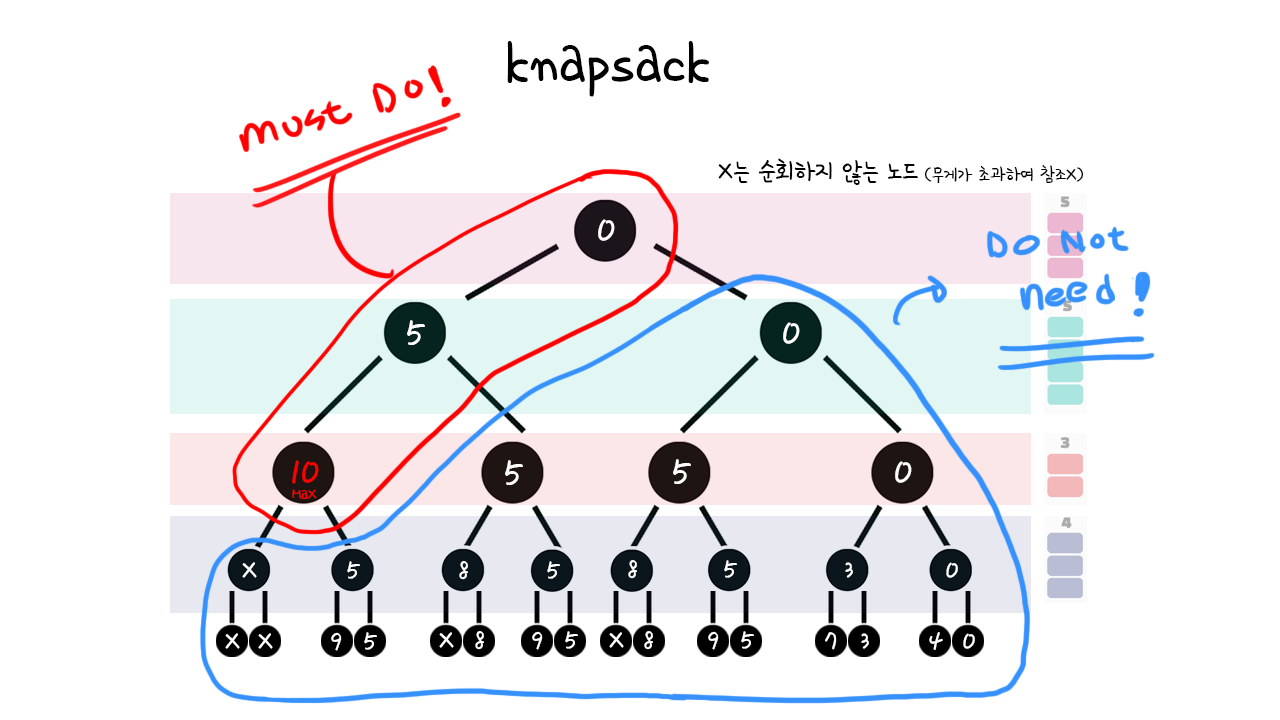
이러한 상황에서 나머지 순회를 돌아야 할까요? 위 그림에서 보듯이 정답을 찾기 위해서는 2번의 노드 순회만 있으면 무관합니다. 나머지는 필요가 없지요. 하지만 우리는 나중의 순회에서 더 비싼 값이 나올지, 낮은 값이 나올지의 대해서 알 방법이 없기 때문에, 계속해서 순회를 돌 수밖에 없을 것입니다.

만약 나머지 순회를 돌 필요가 없다고 판단된다면 알고리즘의 비용은 상당히 줄어들 것입니다. knapsack알고리즘의 개선은 이러한 생각에서 출발합니다.
다음글에서 이어집니다...
ps)
참고 :
'알고리즘 5+1' 카테고리의 다른 글
| Knapsack Problem(3) - 알고리즘 짚어보기 (0) | 2021.05.14 |
|---|---|
| Knapsack Problem(2) - 근사 알고리즘 적용하기 (0) | 2021.05.10 |
| 탐욕 알고리즘(2) - (greedy 알고리즘 활용 - 강의실 배정문제 ) (0) | 2021.04.21 |
| 탐욕 알고리즘(1 - greedy 알고리즘 소개) (0) | 2021.04.15 |
| 트리 알고리즘 (4- 트리의 순회방법 (정리편)) (0) | 2021.04.07 |