
○들어가는 글
저번 시간에는 분할 정복법의 대해서 알아보았습니다. 분할 정법이 무엇이고, 또 그리디와의 공통점, 차이점을 들어가면서 이를 더 다뤄봤었습니다.
이번 시간에는 저번에 우리가 예제를 들었던 피보나치수열 문제를 알아보고, 구현해 보는 시간을 가져보도록 하겠습니다. 추가로 이진트리도 다뤄보고, 마지막으로 분할 정복법의 대한 총정리까지 마치면서, 이번 시작을 마치려고 합니다.
○ 문제1) 피보나치 수열 구현

피보나치수열을 구현해 봅시다. 저번 시간에서 여러 번 다뤘지만, 다시 한번 피보나치의 구조를 다시 한번 봅시다.

피보나치는 위와 같이 재귀적인 구조이고, 이러한 문제를 작게 쪼개어 풀고 다시 합치는 것으로 문제를 해결할 수 있다고 하였습니다. 이 부분의 대한 자세한 설명은 이전 글에 있습니다.
그렇다면 분할 정복의 대한 문제는 어떻게 풀어야 할까요? 크게 어려운 것은 없습니다. 그냥 재귀 문제를 푼다고 생각해 보세요. 한번 차근차근 풀어봅시다.
1. 점화식 구하기
우선 점화식을 구해야 합니다. 점화식이 무엇이냐 하면 항과 항 사이들의 관계인데. 쉽게 풀이하면 각 문제들의 규칙입니다.

풀이해봅시다. 분할 정복 알고리즘은 재귀 구조이면서, 또 큰 문제가 작은 문제로 나누어지는 구조입니다. 작은 문제로 나누어지는데 이 나누어지는 과정에서 각 문제들이 서로 다른 규칙을 가지는 것이 아니라, 일정한 규칙을 가집니다. 사실상 재귀를 안다면 당연한 사실이지요.
문제들이 일정하게 가지고 있는 규칙을 식으로 표현한 것을 점화식이라고 표현할 수 있을 것입니다. 이 것을 구하는 것이 어떻게 보면 재귀와 분할 정복의 핵심입니다.
그렇다면 한번 피보나치의 점화식을 구해봅시다. 사실 이러한 것은 관찰력이 중요합니다. 한번 피보나치수열을 표현해 봅시다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ……... 1 + 1 = 2 1 + 2 = 3 2 + 3 = 5 3 + 5 = 8 5 + 8 = 13 8 + 13 = 21 13 + 21 = 34 21 + 34 = 55 |
이를 함수로 표현해 봅시다. 그렇다면 다음처럼 될 것입니다.

이 정도쯤 된다면 규칙이 쉽게 보일 것입니다. 각 함수의 인자를 보았을 때, 피보나치의 수는 다음과 같은 점화식을 가지고 있다고 볼 수 있습니다.
| fibo(n) = fibo(n-2) + fibo(n-1) |
이것이 피보나치 수의 점화식입니다. 즉 점화식 이기 때문에 모든 피 보나 치수는 위의 조건을 모두 만족하게 됩니다. 이는 분할 정복 핵심이기도 합니다.

2. 바닥 조건 구하기
또한 바닥 조건이 필요합니다. 재귀는 바닥 조건이 없으면 무한으로 재귀를 호출해서 결국에는 스택 오버플로우가 발생할 것입니다. 그것을 방지하기 위해서라도 바닥 조건은 필수입니다..
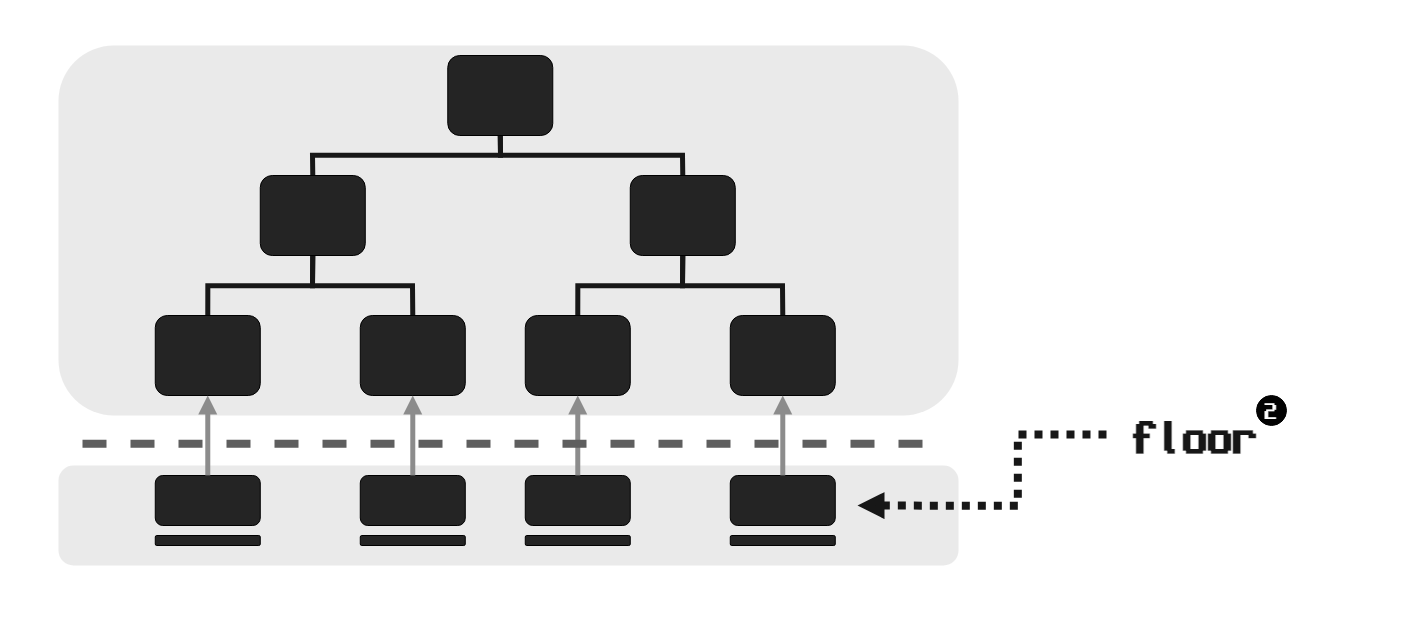
우선 피보나치수열은 2개의2 수를 더함으로써 만들어지는 수입니다. 즉 적어도 연산을 위해서는 기본적으로 값 2개는 주어져야 합니다.
만약 다음과 같은 피보나치 수를 구하는 점화식, 내지 함수가 있다고 하겠습니다.
| fibo(n) = fibo(n-2) + fibo(n-1) |
그리고 한번 피보나치수열을 한 번 봅시다.

여기에서 2부터 (즉 3번째 피보나치 수 == fibo(3))는 위에서 설정한 점화식을 사용할 수 있습니다. 3의 경우 n-1과n -2의 값이 존재할 수 있기 때문입니다. 하지만 그 이하( fibo(1) , fibo(2) )는 구할 수 없습니다. 이럴 경우의 점화식은 다음과 같아지기 때문입니다..
fibo(1) = fibo(-1) + fibo(0)
fibo(2) = fibo(0) + fibo(1)
피보나치 수 중에 00 이하의 수는 없습니다. fibo(-1)와fibo(0)는 구할 수 없다는 것이지요. (사실 fido(2)의 경우 엄밀히 말하자면 “0 + 1 = 1” 이긴 합니다만, 정의하지 않았다는 가정하에 우선 넘어가 봅시다. )
그렇다면 이를 바닥 조건으로 활용하는 것이 가능할 것입니다.
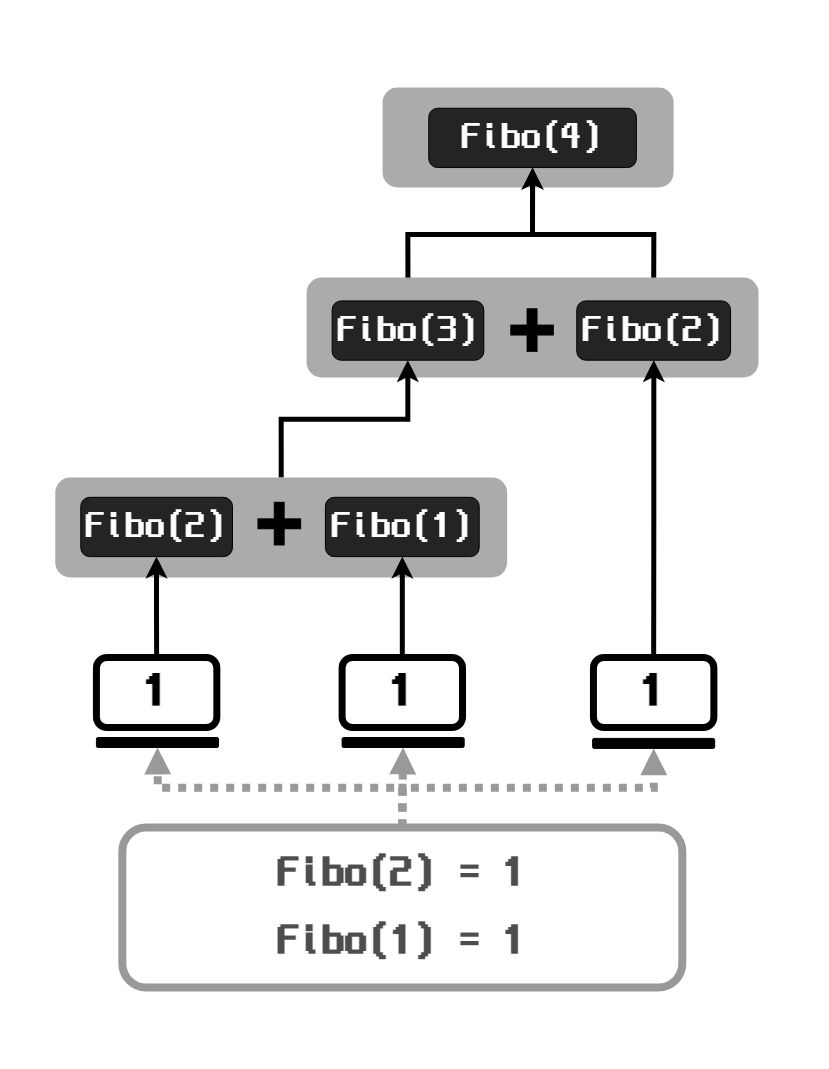
만약 재귀가 일어나는 도중, 만약 fibo(1) fibo(2)의 값을 구하고자 한다면 모두 1을 반환하는 것으로 해결할 수 있을 것입니다.
fun fibo(num : Int) : Int {
if(num==1) return 1 // 바닥조건을 추가합니다.
if(num==2) return 1 // 바닥조건을 추가합니다.
return fibo(num-1) + fibo(num-2)
}미리 어느 정도 바닥 조건을 정의하면, 재귀를 끝마칠 수도 있고, 가장 작은 문제를 해결한 것이기 때문에 이를 통해 큰 문제들 즉, fibo(3) fibo(4) … fibo(10) 이런 식으로 큰 문제를 풀 수 있을 것입니다.
○ 구현하기
한번 구현해 봅시다. 우선 가장 큰 목표는 피보나치 수 1개를 구하는 함수를 만드는 것입니다.
fun fibo(num : Int) : Int {
if(num==1) return 1 // 바닥조건 1
if(num==2) return 1 // 바닥조건 2
}우선 함수를 만들고 바닥 조건을 정의해 줍니다. 조건이 fbo(1) , fibo(2) 일 때는, 모두 1을 반환하도록 조건을 정의했습니다. 이렇게 하면 재귀가 끝나면서 작은 문제가 됩니다.
fun fibo(num : Int) : Int {
if(num==1) return 1 // 바닥조건 1
if(num==2) return 1 // 바닥조건 2
return fibo(num-1) + fibo(num-2) // 점화식
}그리고 점화식을 구현해 줍니다. 바닥 조건이 아닐 때에는 점화식을 통해서 나머지 작은 문제들의 결과 값을 합쳐서 최종 해를 만들 수 있을 것입니다. 그림으로는 다음과 같이 설명할 수 있을 것입니다.
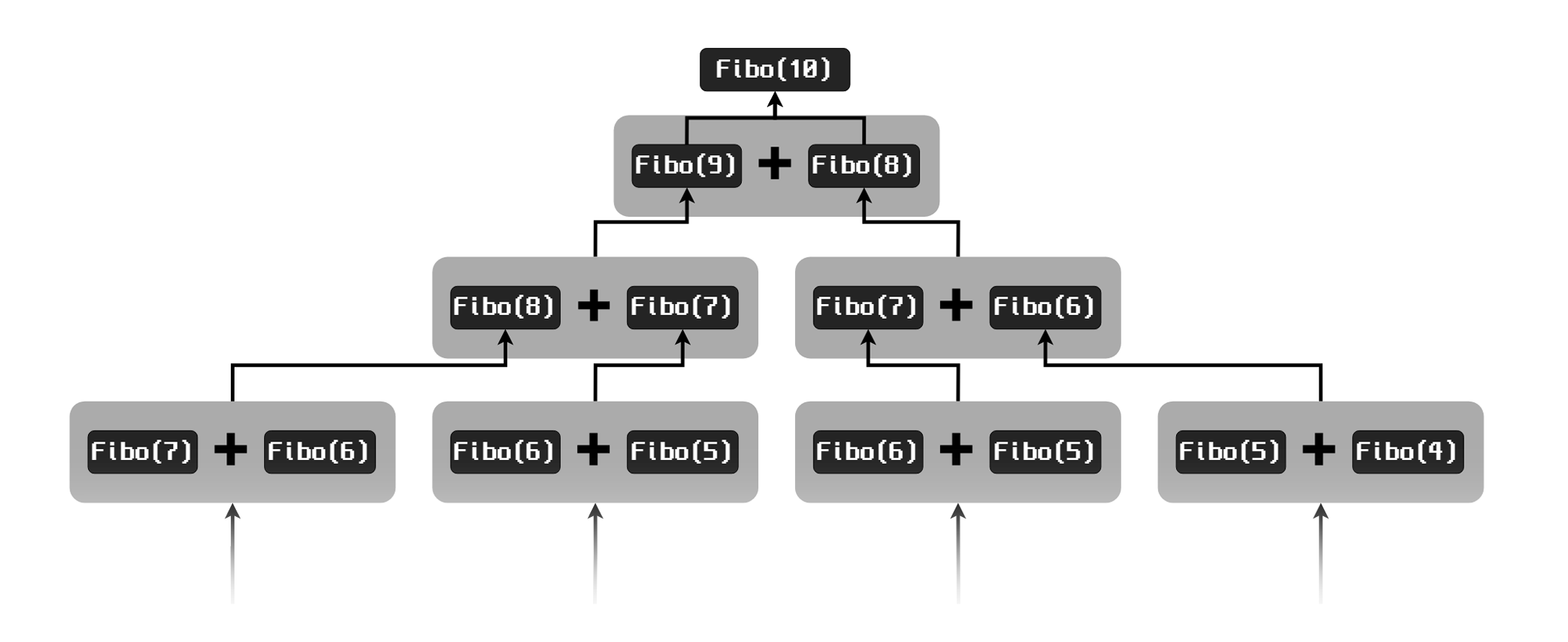
전체 코드는 다음과 같습니다.
fun main() {
val n = 10
println(fibo(n))
}
fun fibo(num : Int) : Int {
if(num==1) return 1 // 바닥조건1
if(num==2) return 1 // 바닥조건2
return fibo(num-1) + fibo(num-2) // 점화식
}결과는 다음과 같습니다.
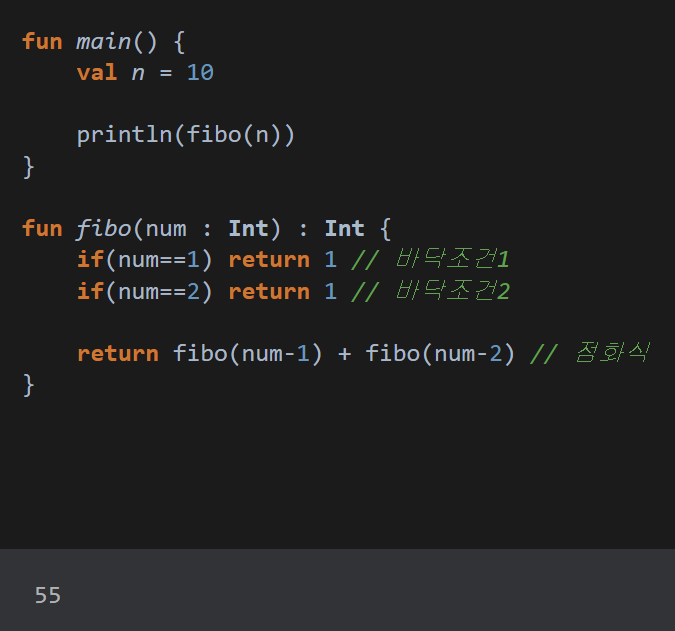
○ 문제 2)이진트리의 구현
재귀적인 구조라면 이진트리 구조도 구현할 수 있을 것입니다. 사실 이미 저희는 구현해 본 적이 있습니다.
https://kuck-su-labor.tistory.com/50
트리 알고리즘 (1 - 개요)
○들어가는 글 우선 이번 시간에는 알고리즘 중, 우리에게 흔히 배낭 문제라고 알려진 knapsack 알고리즘의 대해서 다뤄보려고 하였습니다. 나중에 글을 쓰겠지만 트리를 이용해서 모든 노드를
kuck-su-labor.tistory.com
위의 글에서 우리는 이진트리를 재귀 적으로 구현해 본 적 있습니다. 노드의 한쪽은 값을 +1 하는 노드, 다른 한쪽은 그냥 통과하는 알고리즘이었습니다. 그림으로 표현하면 다음과 같습니다.
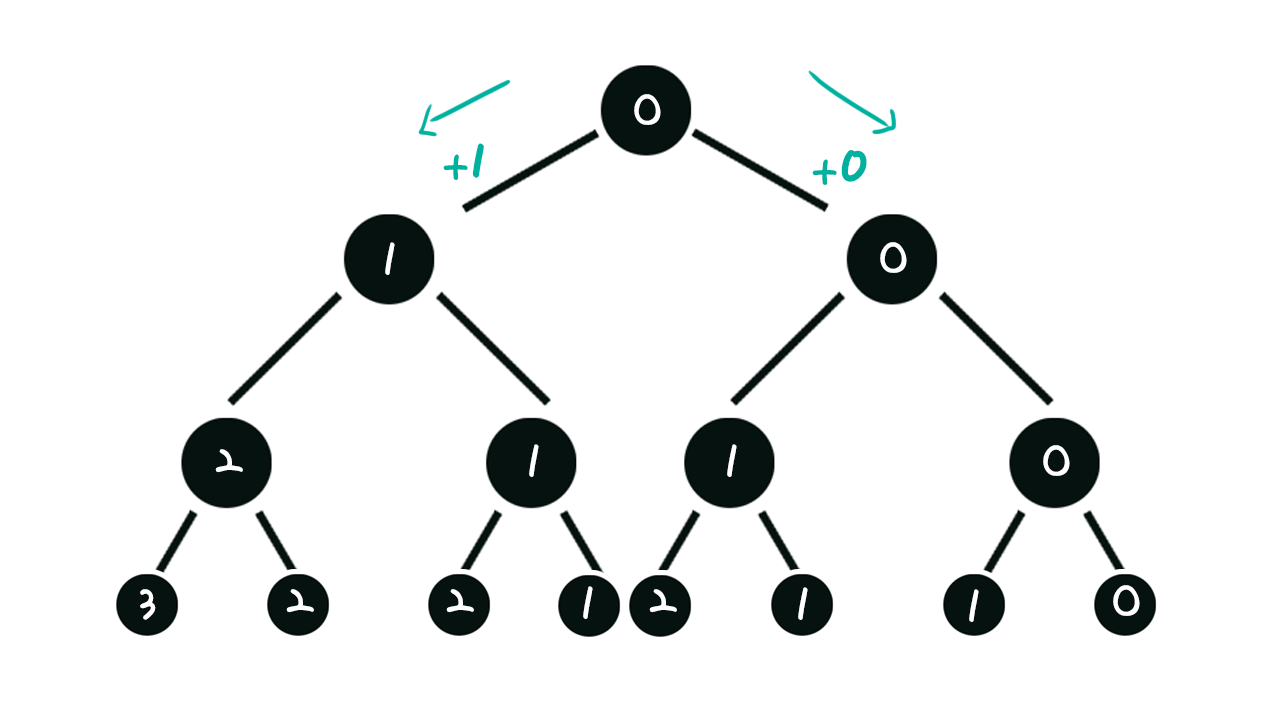
코드로는 다음과 같이 구현할 수 있을 것입니다.
fun main() {
val n = 3
tree(0,n,0)
}
fun tree(num : Int, h : Int, idx : Int) {
if(h==idx) {
print("$num ")
return
}
tree(num+1,h,idx+1)
tree(num,h,idx+1)
}
○ 정리

- 분할 정복법은 그리디 알고리즘과 어느 정도 공통점이 있다.
- 그리디와 분할 정복법은 쪼개 작은 단위로 문제를 해결하고 합쳐서 해결한다는 공통점이 있다. ( 최적 부분 구조(Optimal Substructure) )
- 그리디와 분할 정복법 중에서 그리디와 달리 분할 정복법은 재귀적인 문제를 해결하는 차이점이 있다. ( 중복된 하위 문제(Overlapping Subproblems) )
- 분할 정복은 다음과 같은 순서로 문제를 해결할 수 있다.
- 분할 - 큰 문제를 작은 문제로 나눈다.
- 정복 - 작은 문제를 해결한다. ( == 점화식을 도출한다. )
- 조합 - 작은 문제의 해를 합친다.
- 분할 정복은 재귀적인 구조를 해결하는 알고리즘이다.
- 분할 정복법은 중복된 하위 문제(Overlapping Subproblems)와 최적 부분 구조(Optimal Substructure)의 구조를 가진 문제를 풀 수 있다.
○ 분할 정복법의 문제
여기까지 분할 정복법의 대해서 알아보았습니다. 하지만 우리가 아직 하나 간과한 것이 있습니다. 그것은 바로 비용입니다. 재귀적인 구조는 계속된 재귀 호출 때문에 시간적으로도, 공간적으로도 비용이 많이 들게 됩니다. 따라서 효율적이지는 않지요.
때문에 우리는 예전에 최근접 알고리즘을 활용해, 불필요한 재귀를 줄임으로써, 알고리즘을 개선시킨 적이 있었습니다. 하지만, 이 방법은 항상 좋은 효율을 보장하지는 않고, 또 구현 과정에서 제한사항이 있습니다.
Knapsack Problem(1) - (재귀로 구현하기)
○들어가는 글 우리는 지금까지 tree(이진 트리) 알고리즘과 greedy 알고리즘을 알아보았습니다. 이제 우리는 이 2가지 알고리즘 (이진트리 + 근사 알고리즘) 을 이용해서 좀 더 효율적인 knapsack 알
kuck-su-labor.tistory.com
분할 정복에서 우리는 큰 문제의 대한 값을 얻기 위해서, 작은 문제를 재귀적으로 호출해서 답을 얻습니다. 문제는 만약 이전의 호출했던 값을 한번 더 호출을 한다고 하더라도, 또다시 재귀적인 호출을 일일이 해서 답을 얻어야 한다는 것입니다. 이것이 가장 큰 문제입니다.
예를 들어 봅시다. 우리는 지금까지 피보나치 1개의 수를 출력하는 것을 이야기했지만, 코드처럼 수열을 출력하는 경우를 봅시다. 피보나치 수 1부터 10까지 출력한다고 했을 때, 우선 바닥 조건인 fibo(1)과 fibo(2)를 출력할 수 있을 것입니다.

다음은 피보나치수열 3번째인 fibo(3). 이것은 fibo(1)과 fibo(2)의 합입니다. 우리는 이전에 이를 바닥 조건으로 지정했었고, 각 결과가 1인것을 알고 있습니다. 재귀가 필요 없이 바로 fibo(1)과 fibo(2)를 구해서 fibo(3)를 구할 수 있습니다.

문제는 그 이후부터입니다. 우리는 fibo(1) ~fibo(3)의 값을 알고 있지만, 위 코드라면 그런 것과는 상관없이 fibo(1), fibo(2), fibo(3)을 계속해서 호출하게 될 것입니다.
그 말은 즉, fibo(4), fibo(5)등 이후부터는 우리는 이미 값을 알고 있지만, 그것과는 상관없이 계속해서 재귀가 일어나게 된다는 뜻입니다. 이는 비효율적입니다.
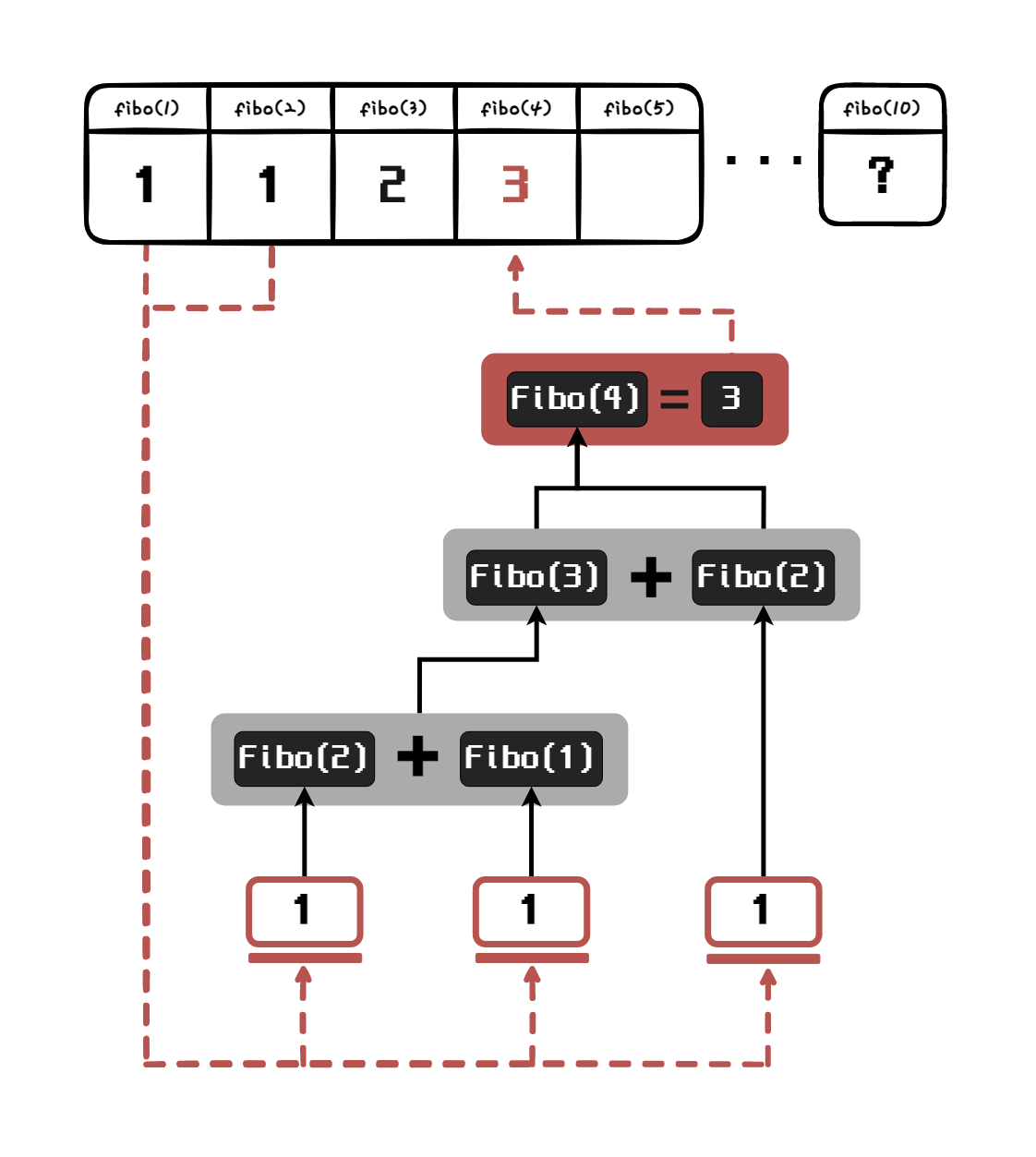
만약 이러한 중복된 값을 어디엔가 저장해 놨다가, 다시 한번 사용하면 굳이 재귀를 수행할 필요는 없지 않을까요? 이미 구한 값이면 재귀를 수행해서 바닥 조건까지 갈 필요 없이 바로 값을 불러올 수 있으면 좋을 것 같습니다.

위 그림을 보면 fibo(3)을 이미 구했다는 가정하에, fibo(3)을 재귀로 다시 구하는 대신 저장된 fibo(3)의 해인 2를 불러오는 것을 알고 있습니다. 이렇게 되면 각 점회식이 구해야 하는 재귀 과정을 생략하고 구하는 것이 가능합니다.
아래 그림은 위 그림을 좀 더 간단하게 나타낸 그림입니다. 아래 그림과 위 그림은 개념적으로는 같습니다.

이렇게 이미 구한 값이라면, 재귀과정을 생략함으로써 알고리즘을 효과적으로 동작시킬 수 있습니다.
동적 계획법 (Dynamic Programming, DP)은 이러한 알고리즘은 재귀를 가능한 사용하지 않고 동작 함으로써, 알고리즘 효율을 극대화시킬 수 있습니다. 동적 계획법은 이러한 아이디어에서 출발합니다.
다음 글에서 이어집니다...
'알고리즘 5+1' 카테고리의 다른 글
| 동적계획법 [Dynamic Programming - DP](2) - 실전편 (2) | 2022.02.02 |
|---|---|
| 동적계획법 [Dynamic Programming - DP](1) - 개념편 (0) | 2022.01.23 |
| 분할정복법 [Divide & Conquer] (1 - 이론편 ) (0) | 2021.08.24 |
| 예상 대진표 문제 (3) - 비트연산과 이진트리 (0) | 2021.07.14 |
| 예상 대진표 문제 (2) - 이진법 풀이 (0) | 2021.07.10 |