
○ 이어가는 글
https://kuck-su-labor.tistory.com/64
위 글에서 이어집니다.
○ 들어가는 글
우리는 이전까지 알고리즘을 짚어보면서 어떻게 동작하는 지의 대해서 알아보았습니다. 이번 시간에는 이러한 알고리즘을 직접 구현해보도록 하겠습니다.
○ 1. 완전 탐색 트리 구현
이 부분은 우리가 구현해 본 적이 있었습니다. 크게 달라지는 부분은 없기 때문에 이 부분은 생략하도록 하겠습니다. 자세한 내용은 이전글을 참조해 주세요
이전 글 : https://kuck-su-labor.tistory.com/61
우선 구현하면 다음처럼 될 것입니다.

var MaxV : Int = 0
fun main() {
val K : Int = 7 // 가방의 크기
val WnV = mutableListOf(3 to 5, 4 to 5, 2 to 3 , 3 to 4) // 각각의 아이템 -> Pair<무게,가치>
WnV.sortByDescending{ it -> it.second.toFloat() / it.first.toFloat() } // 정렬을 한다. (가치/무게)를 내림차순으로
println("아이템 : $WnV \n")
print("순회 : ")
Knapsack(WnV,7,0,0)
println("\n")
println("최댓값 : $MaxV")
}
// 재귀로 구현하는 완전탐색
fun Knapsack(VA : MutableList<Pair<Int, Int>> , K : Int , i : Int , VM : Int) : Int { // 리스트(요소), 총 무게, 인덱스, 축척된 가치
if(K < 0) return 0 // 무게를 초과하지 못하도록 하기 위해서
print("-> $VM ")
if(K <= 0 || i >= VA.size) {
if(VM> MaxV) MaxV = VM // 기존의 최댓값과 비교하면서 더 큰 최댓값이 있다면 변경한다.
return 0
}
Knapsack(VA,K-VA[i].first,i+1,VM+VA[i].second) // 노드의 좌측방향 (물건을 담는경우)
Knapsack(VA,K,i+1,VM) // 노드의 우측방향 (물건을 담지 않는 경우)
return 0
}
○ 2. 정렬
Greedy 알고리즘을 구현하기 위해서 정렬을 할 수 있도록 코드를 추가해 줍니다. 가성비 순으로, 즉 가치를 무게로 나눈 값대로 내일차순 정렬을 해야 하는데 코틀린이 정말 편리한 게 이러한 부분은 다음과 같이 구현할 수 있습니다.

추가해 줍시다. 이렇게 되면 다음과 같이 가성비 순으로 정렬이 완료됩니다. 순회도 확인해 봅시다.

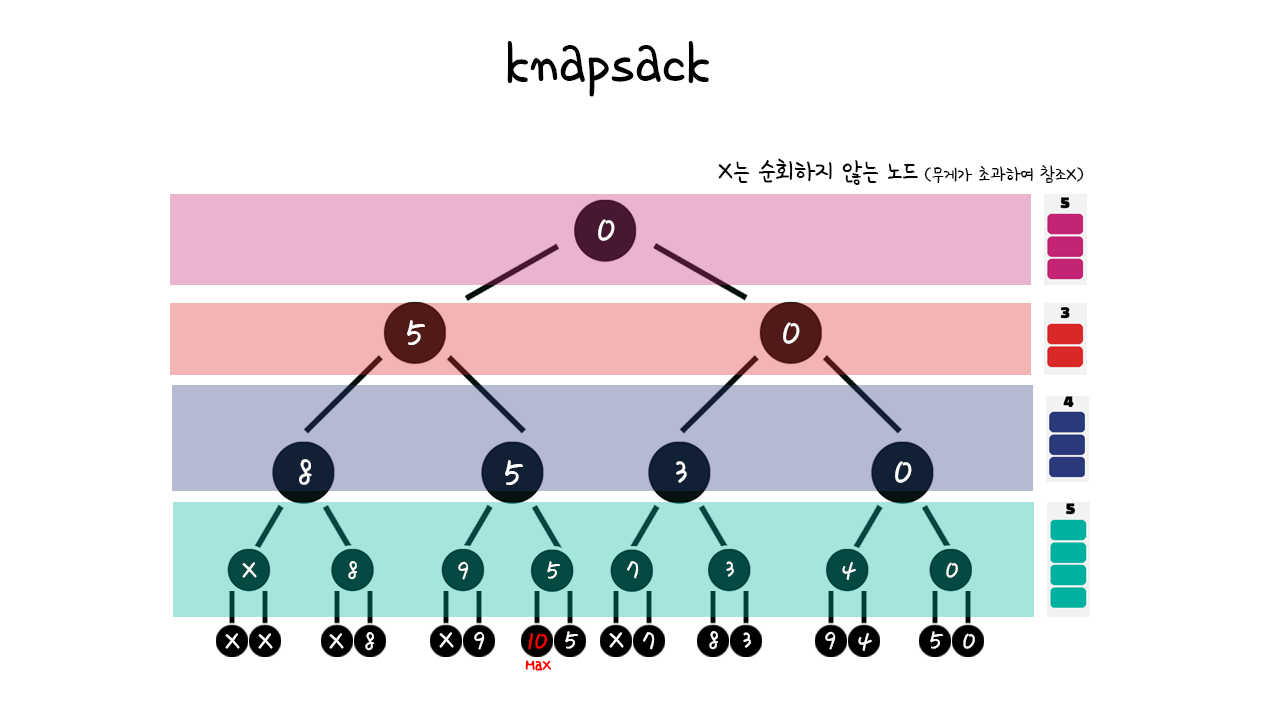
○ 3. 예상 가치 최댓값을 구하는 코드 추가
예상할 수 있는 예상 가치 최댓값을 구해야만 합니다. 다음과 같은 코드를 작성하였습니다.

우선 예상 가치 최댓값을 구하는 과정에서 무게를 담을 변수 Wtotal 과 예상 가치 최댓값 preV을 만들었습니다. 그리고 아직 담지 않은 요소를 순회하기 위해서 받은 인덱스부터 끝까지 요소를 순회합니다.

순회하는 과정에서 2가지 경우로 나뉠 수 있습니다. 우선 요소를 담을 수 있을 만큼의 충분한 공간이 있는 경우입니다. 이러한 경우에는 그냥 공간에 담으면 됩니다. 공간을 얼마만큼 사용하는 지를 나타내기 위해서 Wtotal에 무게를 할당하고, 예상 가치 값 preV에 가치를 할당합니다.
다른 하나의 경우는 요소를 담을 수 없을 만큼의 충분한 공간이 없는 경우입니다. 요소의 가성비(가치/무게)를 남은 무게만큼 담으면 됩니다.
마지막으로 현재 노드까지 구한 가치를 더해주면 예상 가치 최댓값을 구할 수 있습니다. 코드는 다음과 같습니다.
fun FKnapsack(VA : MutableList<Pair<Int, Int>>, K : Int , i : Int , VM : Int ) : Int { // 리스트(요소), 총 무게, 인덱스, 축척된 가치
var Wtotal = 0 // 공간의 사용
var preV = 0 // 예상 가치 값 (VM을 제외한)
for( I in i .. VA.size -1 ){ // i - 1 의 요소는 우리가 방금 담은 요소이다.
if( Wtotal + VA[I].first <= K){ // 요소를 담을 수 있을 만큼 충분한 공간이 있을 경우
Wtotal += VA[I].first
preV += VA[I].second
}
else{
preV += ( VA[I].second / VA[I].first ) * (K - Wtotal) // 요소를 담을 수 있을 만큼 충분한 공간이 없을 경우, (나머지를 가성비로 채운다.)
}
}
return preV + VM // 지금까지 구한 가치를 더해야 온전한 예상 최대 가치가 나온다.
}
○ 4. 재귀 함수에 조건 추가
마지막으로 재귀를 실행하는 함수에 3번의 함수를 추가합니다. 이렇게 하면 매 노드를 순회하면서 예상 가치 최댓값을 구하게 됩니다.

이렇게 구해진 예상 가치 최댓값을 가치 최댓값 MaxV과 비교해서 만약 예정 가치 최댓값이 가지 최댓값보다 작다면, 앞으로의 순회에서 MaxV 보다 큰 값이 나올 일은 없기 때문에 순회를 종료해도 상관없습니다. 따라서 순회를 종료합니다.
○ 결과
코드를 모두 작성하면 다음과 같습니다.
이전 알고리즘과 비교하면 순회가 줄었다는 것을 알 수 있습니다. 이는 요소의 값이 많아지면 많아질수록 순회는 상당히 줄어들게 됩니다.
var MaxV : Int = 0
fun main() {
val K : Int = 7 // 가방의 크기
val WnV = mutableListOf(3 to 5, 4 to 5, 2 to 3 , 3 to 4) // 각각의 아이템 -> Pair<무게,가치>
WnV.sortByDescending{ it -> it.second.toFloat() / it.first.toFloat() } // 정렬을 한다. (가치/무게)를 내림차순으로
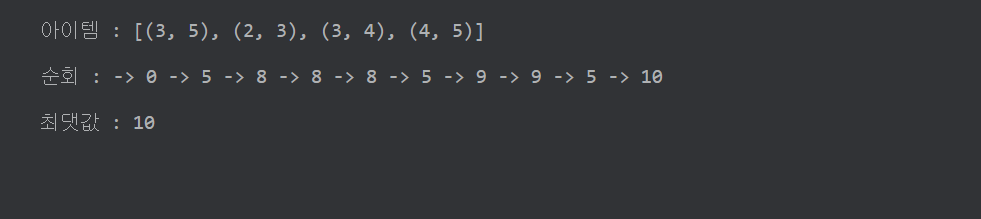
println("아이템 : $WnV \n")
print("순회 : ")
Knapsack(WnV,7,0,0)
println("\n")
println("최댓값 : $MaxV")
}
// 재귀로 구현하는 완전탐색
fun Knapsack(VA : MutableList<Pair<Int, Int>> , K : Int , i : Int , VM : Int) : Int { // 리스트(요소), 총 무게, 인덱스, 축척된 가치
if(K < 0) return 0 // 무게를 초과하지 못하도록 하기 위해서
if( FKnapsack(VA,K,i,VM) <= MaxV ) return 0
print("-> $VM ")
if(K <= 0 || i >= VA.size) {
if(VM> MaxV) MaxV = VM // 기존의 최댓값과 비교하면서 더 큰 최댓값이 있다면 변경한다.
return 0
}
Knapsack(VA,K-VA[i].first,i+1,VM+VA[i].second) // 노드의 좌측방향 (물건을 담는경우)
Knapsack(VA,K,i+1,VM) // 노드의 우측방향 (물건을 담지 않는 경우)
return 0
}
fun FKnapsack(VA : MutableList<Pair<Int, Int>>, K : Int , i : Int , VM : Int ) : Int { // 리스트(요소), 총 무게, 인덱스, 축척된 가치
var Wtotal = 0 // 공간의 사용
var preV = 0 // 예상 가치 값 (VM을 제외한)
for( I in i .. VA.size -1 ){ // i - 1 의 요소는 우리가 방금 담은 요소이다.
if( Wtotal + VA[I].first <= K){ // 요소를 담을 수 있을 만큼 충분한 공간이 있을 경우
Wtotal += VA[I].first
preV += VA[I].second
}
else{
preV += ( VA[I].second / VA[I].first ) * (K - Wtotal) // 요소를 담을 수 있을 만큼 충분한 공간이 없을 경우, (나머지를 가성비로 채운다.)
}
}
return preV + VM // 지금까지 구한 가치를 더해야 온전한 예상 최대 가치가 나온다.
}
○ 알고리즘의 분석
우리는 지금까지 재귀를 이용한 완전 탐색 알고리즘에 Greedy알고리즘을 대입하여, knapsack알고리즘을 개선해 보았습니다. 하지만 약간의 의문점이 드는 사람들도 있을 것입니다.
1. 추가적으로 Greedy 알고리즘을 수행하는 과정은 계산과정에 포함되므로, 비용에는 변화가 없을 것이다.
2. 만약 마지막 리프노드가 정답이었을 경우 이러한 알고리즘은 소용이 없을뿐더러 역효과이다.
3. 더 좋은 알고리즘이 있다.
우선 이것의 대한 답으로는 다음과 같습니다.
1. 우선 답변으로는 “아니다”입니다. greedy 알고리즘의 시간복잡도는 O(n)에 가깝습니다. 이는 완전탐색의 비해서 빠르기 때문에 효과가 있다고 말할 수 있습니다.
2. 우선 답변으로는 “절반은 그렇다”입니다. 만약 완전탐색 기준으로 마지막 리프 노드가 정답이었다면, greedy 알고리즘까지 수행하기 때문에 오히려 역효과입니다. 하지만 실제 구현 과정에서 우리는 한번 정렬을 할 수 있습니다. 정렬된 상태에서는 적어도 마지막 리프 노드가 정답이 있을 확률을 매우 적습니다.
3. 우선 답변으로는 “그렇다”입니다. 저도 실제 구현해 봤을 때 이러한 알고리즘의 차이가 느껴지려면 사용되는 값이 많을 때의 이야기입니다. 그리고 보통은 DP알고리즘이 이 알고리즘에 더 빠른 것 같았습니다. 반례는 없지만, 다른코드도 보았을 때 대체로 그런 것 같았습니다.
○ 이번 글을 마치면서
드디어 knapsack알고리즘을 알아보았습니다. 재귀적으로 알고리즘을 구성하는 것부터 순회를 줄이는 방법까지 순서대로 알아보았습니다.
이렇게 효율적인 알고리즘의 대해서 생각하고, 고민하는 것은 프로그래머의 사명인 것 같습니다. 사실 knapsack알고리즘도 DP 알고리즘으로 구현한다면 더 좋을지도 모르겠습니다.
다음은 아직 정해진 것은 없지만, 말이 나온 김에 DP알고리즘의 대해서 알아보고 싶기도 하고, 요즘 정렬의 대해서 좀 알아보고 싶기 때문에 힙 정렬의 대해서도 다뤄보고 싶습니다. 아마 이 둘 중에서 하나를 선택할 것 같습니다. 다음에는 이러한 새로운 알고리즘을 가져오도록 하겠습니다. 감사합니다.
'알고리즘 5+1' 카테고리의 다른 글
| Kotlin diary (2) - 스트림 함수들 (0) | 2021.06.16 |
|---|---|
| Kotlin diary (1) - 자주 사용했던 것들 (0) | 2021.05.30 |
| Knapsack Problem(3) - 알고리즘 짚어보기 (0) | 2021.05.14 |
| Knapsack Problem(2) - 근사 알고리즘 적용하기 (0) | 2021.05.10 |
| Knapsack Problem(1) - (재귀로 구현하기) (0) | 2021.04.30 |